8.Sınıf LGS Matematik Deneme Sınavı 18

Sude her hafta bir önceki haftaya göre 10 lira fazla olacak şekilde kumbarasına para atmaktadır. Aşağıda ilk 3 hafta kumbarasına attığı para miktarı lira cinsinden gösterilmiştir.

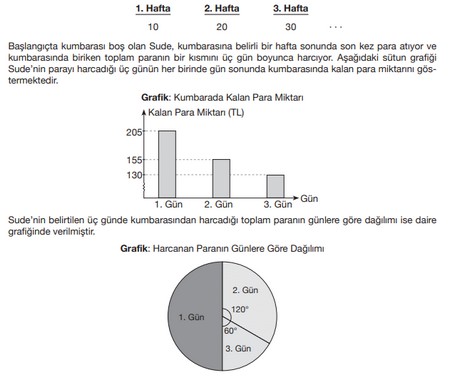
Buna göre Sude kaçıncı hafta sonunda kumbaraya para atmayı bırakmıştır?

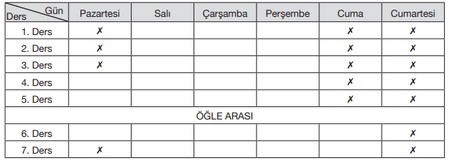
Bu programda Fatih Öğretmen’in pazartesi, cuma ve cumartesi günleri girdiği dersler “✗” ile işaretlenmiştir. Diğer günlerde girdiği ders sayılarıyla ilgili aşağıdakiler bilinmektedir:

• Salı ve perşembe eşit sayıda derse girmiştir.

• En az sayıda derse girdiği gün çarşambadır.

Buna göre haftalık ders saati sayısı 29 olan Fatih Öğretmen’in çarşamba günü rastgele seçilen bir ders saatinin boş olma olasılığı en az kaçtır?

Aşağıda iki eş bölümden oluşan dikdörtgen biçiminde bir yemek masası gösterilmiştir.

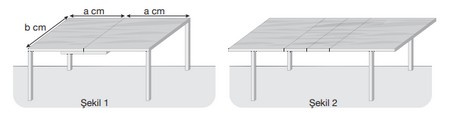
Bu yemek masasının ortasında yer alan gizli bölmede her iki tarafa da eşit miktarda açılabilen ek bölümler vardır. Şekil 2’deki gibi bu ek bölümler açıldığında masanın üst yüzeyinin alanı (4ab – 2b²) cm² olmaktadır.

Buna göre ek bölümlerden birinin santimetre cinsinden çevre uzunluğunu veren cebirsel ifade aşağıdakilerden hangisidir?

Kerem yurt dışında yapılan özel bir satranç turnuvasına katılmıştır. Bu turnuvaya katılan yarışmacılara birer yaka kartı verilmektedir. Aşağıda bu turnuvaya katılan Kerem’in kare biçimindeki yaka kartı gösterilmiştir.

Bu yaka kartında, alanı 12 cm² olan dikdörtgen biçiminde bir bayrak bölümü vardır. Bu bölümün kenar uzunlukları oranı 'dir.

Yaka kartının kenar uzunlukları santimetre cinsinden birer doğal sayı olduğuna göre çevre uzunluğu en az kaç santimetredir?

Kenar uzunlukları a ve b olan dikdörtgenin alanı a.b’dir.

Aşağıda bir okulun Atatürk köşesinde kullanılan ikisi eş olmak üzere toplam üç tane dikdörtgen biçiminde çerçeve gösterilmiştir.

Kenar uzunlukları santimetre cinsinden 60’tan küçük birer tam sayı olan bu çerçevelerin ön yüzlerinin alanı 2000 cm² ile 2200 cm² dir.

Çerçevelerin kısa kenar uzunlukları eşit olduğuna göre Atatürk çerçevesi diğer çerçevelerden en az kaç santimetre uzundur?

1 m = 100 cm

Yapılan araştırmalara göre bir kişinin kol açıklığının (kolların gerilerek yana doğru açılmasıyla oluşan uzunluk) boy uzunluğuna oranı 1’e eşittir.

Hakan, Önder, Onur ve Ali adlı dört arkadaşın santimetre cinsinden boy uzunlukları tabloda verilmiştir.

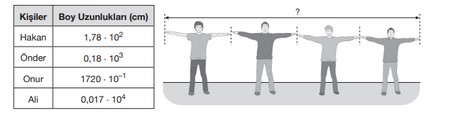
Bu dört arkadaş kollarını yere paralel olacak biçimde açıp parmak uçları aynı hizada yan yana yukarıdaki gibi diziliyor.

Buna göre elde edilen uzunluk (?) kaç metre olur?

a, b ve c birer doğal sayı olmak üzere

Dikdörtgen biçimindeki bir karton aşağıdaki gibi alanları santimetrekare cinsinden tam sayı olan 4 parçaya ayrılıyor.

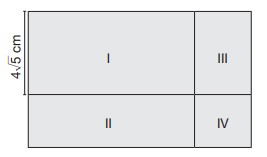
Bu parçalardan II numaralı olan 3 cm genişliğinde eş aralıklara bölünmüş bir sayı doğrusunun üzerine aşağıdaki gibi yerleştiriliyor.

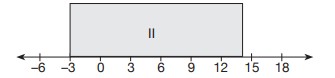
IV numaralı parça kare biçiminde ve alanı 20 cm² olduğuna göre başlangıçtaki kartonun çevre uzunluğu en çok kaç santimetredir?

Bir ayna ustası Şekil 1’de verilen kare biçimindeki aynayı; uzun kenar uzunluğu, kısa kenar uzunluğunun 3 katı olacak biçimde belirtilen şekilde keserek birbirine eş 4 dik üçgen ile 1 kare parça olmak üzere toplam 5 parça elde ediyor. Bu parçalardan 4’ünü kenarları boyunca yapıştırarak Şekil 2’deki ayna sistemini oluşturuyor.

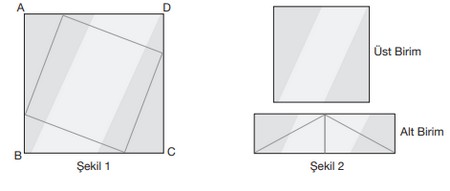
Şekil 2’de elde edilen sistemde alt birimin alanı 270 cm² olduğuna göre üst birimin alanı kaç santimetrekaredir?

a, b ve c birer rakam olmak üzere aşağıda verilen her bir karenin alanı a,bc cm² biçimindedir. Kenar uzunlukları birer rasyonel sayı olan bu karelerin alanları 1 cm² den büyük ve 3 cm² den küçüktür.

Doruk bu karelerden a + b + c toplamı tam kare olanları maviye, tam kare olmayanları ise kırmızıya boyayacaktır.

Örneğin;

alanı 1,44 cm² olan kareyi 1 + 4 + 4 = 9 olduğundan maviye, alanı 2,89 cm² olan kareyi 2 + 8 + 9 = 19 olduğundan kırmızıya boyuyor.

Daha sonra maviye boyadığı en büyük kare ile kırmızıya boyadığı en küçük kareyi aşağıdaki gibi kenarları çakışacak biçimde yapıştırıyor.

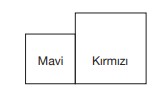
Buna göre Doruk’un elde ettiği şeklin çevre uzunluğu kaç santimetredir?

a ≠ 0 ve m, n birer tam sayı olmak üzere

Laboratuvar ortamındaki boş bir deney tüpü aşağıda gösterilmiştir. 5 eş bölüme ayrılmış bu deney tüpü Şekil 1’deki gibi 100 000 bakteri ile dolduruluyor.

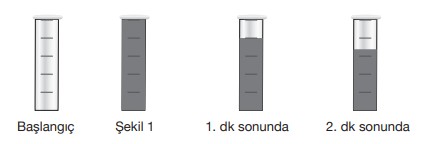
Her bir dakikanın sonunda bu tüpten o anda bulunan bakterilerin ’i alınıyor.

Buna göre 5. dakika sonunda tüpte kalan bakteri sayısı aşağıdakilerden hangisine eşit olur?

(Bu süre boyunca tüpte bulunan bakterilerin çoğalmadığı bilinmektedir.)

a, b, c ve d birer doğal sayı olmak üzere Dikdörtgen biçimindeki bir karton 8 eş bölüme ayrılmıştır. Bu bölümlere şekil 1’de gösterildiği gibi kareköklü ifadeler yazılmıştır.

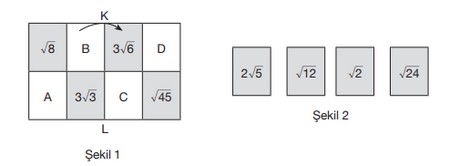
Kartonda boş kalan 4 bölüme ise Şekil 2’de verilen kartlarda yazan kareköklü ifadeler, her bölümde bir kareköklü ifade olacak biçimde yazılacaktır. Bu karton [KL] boyunca ok yönünde kendi üstüne katlandığında üst üste gelen bölümlerdeki kareköklü ifadelerin çarpımının birer doğal sayı olması istenmektedir.

A, B, C ve D bu bölümlere yazılacak kareköklü ifadeler olduğuna göre işleminin sonucu kaçtır?

Alfabemizdeki 29 harf bulunduğu sıranın karekökü ile ilişkilendirilerek aşağıdaki tablo oluşturuluyor.

Bir kelimedeki harflerden karekökü rasyonel sayı olanlar, karekökü irrasyonel sayı olanlardan daha fazla ise “rasyonel kelime” daha az ise “irrasyonel kelime” eşit ise “gerçek kelime” olarak adlandırılıyor.

Örneğin;

Buna göre aşağıdaki kelimelerden hangisi “gerçek kelime”dir?

Adrenalin hormonu, böbrek üstü bezleri tarafından salgılanan bir hormon türüdür. Halk arasında ismi daha çok heyecan verici ve korkutucu durumlarda anılmaktadır. Bunun sebebi bu hormonun salgılanma miktarı normal zamanlarda sabit bir şekilde ilerlerken heyecan, stres, kaygı, korku vb. anlarda salgılanma miktarının artış göstermesidir.

8. sınıf öğrencisi Celal’in Hız Yayınları tarafından yapılan deneme sınavına girdiği bir günde heyecanlı olduğu görülmüştür. Aynı günün belirli saatlerinde Celal’in vücudundaki anlık adrenalin hormonunun miktarı aşağıdaki çizgi grafiğinde gösterilmiştir.

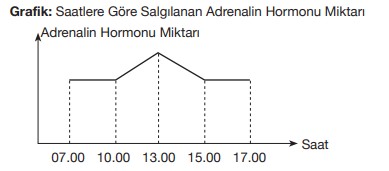
Buna göre belirtilen gün içinde aşağıdaki saatlerden hangisinde Celal’in deneme sınavında olma olasılığı daha fazladır?

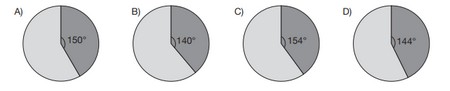
Yeni açılan bir spor salonuna kayıt olan kadın ve erkek üye sayılarının aylara göre dağılımı aşağıdaki sütun grafiğinde gösterilmiştir.

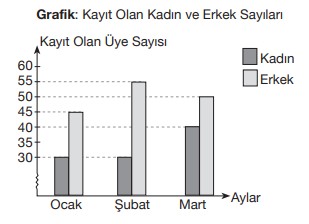
Bu grafiğe göre yılın ilk üç ayı sonunda spor salonuna kayıt olan kadın ve erkek üyelerin toplam sayısının dağılımını gösteren dairesel grafik aşağıdakilerden hangisidir? (Bu üç ay boyunca kaydını sildiren üye olmamıştır.

 

Aşağıda Şekil 1’de dikdörtgen biçiminde bir kağıt gösterilmiştir.

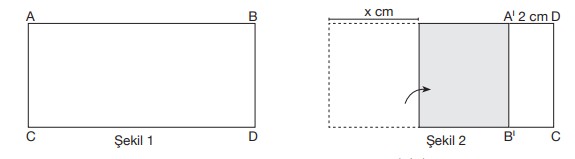
Bu kâğıt kendi üzerine x cm boyunca katlandığında Şekil 2’deki gibi |A'D| = 2 cm olmaktadır.

AıBıCD dikdörtgeninin alanı (4x – 4) cm2 olduğuna göre Şekil 1’deki kâğıdın ön yüzünün santimetrekare cinsinden alanını veren cebirsel ifade aşağıdakilerden hangisidir?

İki takım arasında ve en fazla 5 setin oynandığı voleybol karşılaşmalarında beraberlik olmayıp üç set alan takım oyunu kazanmaktadır.

Buna göre Kadın Milli Voleybol Takımımız’ın Tokyo’daki olimpiyatlarda yapacağı ilk maçın sonucu için kaç farklı olası durum vardır?

Aşağıdaki Şekil 1 ve Şekil 2’deki kareli kağıtlarda santimetre cinsinden çevre uzunlukları birbirine eşit iki dikdörtgen çizilmiştir.

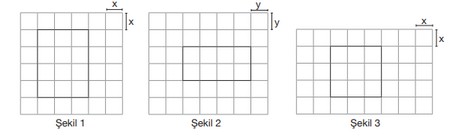
Buna göre Şekil 3’te verilen karenin santimetre cinsinden çevre uzunluğu aşağıdakilerden hangisine eşittir?

Aşağıda Şekil 1 ve Şekil 2’de verilen dikdörtgen biçimindeki kartonlar ikişer kenarları çakışacak biçimde üst üste yapıştırılarak üst üste gelen kısımları boyanıyor.

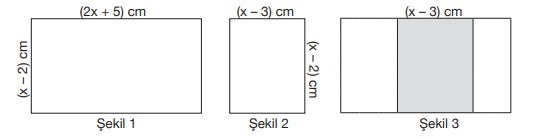
Buna göre Şekil 3’te boyalı olmayan bölgenin santimetrekare cinsinden alanını veren cebirsel ifade aşağıdakilerden hangisidir?

Bir işyeri sahibi aşağıda verilen 2’si kare 1’i dikdörtgen olmak üzere 3 adet seramik çeşidini kullanarak bir duvar süslemesi yapacaktır.

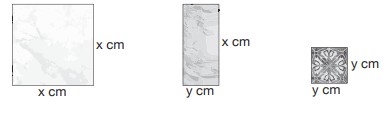
Bu seramikler kullanılarak aşağıdaki duvar süsü oluşturulmuştur.

Buna göre oluşturulan duvar süsünün santimetrekare cinsinden yüzey alanı aşağıdakilerden hangisine eşittir?

Aşağıda bazı şekiller ve bu şekillerin ifade ettiği işlemler verilmiştir.

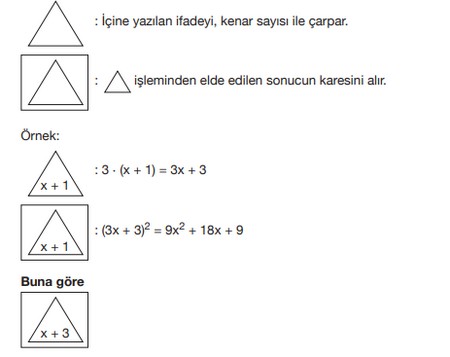
biçiminde tanımlanan işlemin sonucu aşağıdakilerden hangisidir?